Elastics, Plastics and Hooke's Law

Elastics and plastics

Some materials increase in size when stretched, decrease in size when compressed, and snap back to their original shape when the deforming force is withdrawn. Such materials are said to be elastic. If the force exceeds some threshold value however, the materials do not regain their original shape after the deforming force is withdrawn. The point at which this occurs is referred to as the elastic limit (elastic limit is defined as the point beyond which an elastic material does not regain its shape after the deforming force is withdrawn). Examples of elastic materials are rubber, steel, and coils (springs). 

Some materials are permanently deformed as soon as a deforming force is applied. If such a material is expanded for instance, it retains the expanded size even after the expanding force is withdrawn. Such materials are called plastics. A good example of a plastic material is a polythene bag (juala). It is important to note that all elastic materials turn into plastic materials when deformed beyond their elastic limits.

Applications of elastic materials

• Trampoline – when one jump on it, it stretches, then regains its shape.
• Elastic band – used for fastening for example bundles of paper.
• Springs – used in spring balances used for weighing. 
• Clothes – that pair of skinny jeans that fits like a second skin is made using an elastic material

Applications of plastics

• Used for packaging
• Casing of appliances such as phones, toys, cars etc.

Hooke’s law

Hooke’s law states that extension of an elastic material is directly proportional to the force applied to it so long as the elastic limit is not exceeded. Say for example a force F is applied to a spring such that it extends by an amount e (equal to final length, say L, less the original length, say L₀, i.e., L-L₀). 

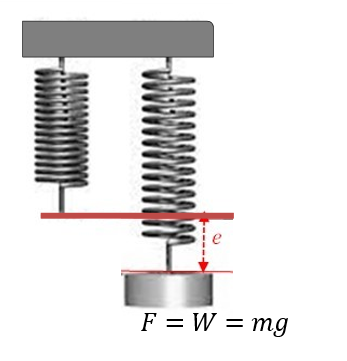
It follows that by Hooke’s law,

                               (i)

                                                            (ii)

k is a constant of proportionality called spring constant; it is a measure of the stiffness of a spring (coil).  A spring that stretches easily has a smaller spring constant compared to a stiffer one and as such reaches the elastic limit sooner. 

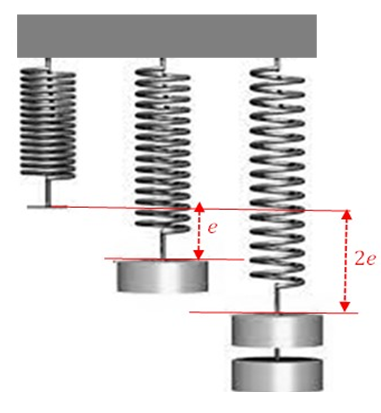
Springs in parallel

Consider two springs of equal length L and spring constants k₁ and k₂ respectively. Suppose that when the two spring are arranged in parallel and a force F applied between them, each spring stretches by an amount e.

The force F is divided equally between the two springs and as such each spring supports a force F / 2. It therefore follows that by Hooke’s law;

Spring 1:

                                                        (iii)

Spring 2:

                                                       (iv)

Total force:

                                                      (v)

The value k₁ + k₂ represents the effective spring constant K of the arrangement, i.e. 

Considering that the two springs are identical, then;

                                             (vii)

                         (viii)

Equation (viii) shows that if two springs in parallel are connected in such a way that they share a common load, the effective spring constant doubles. 

Springs in Series

Suppose that two identical springs are now connected in series and after the load is attached, each spring stretches by an amount e₁ and e₂ respectively. Since both loads are supporting the same load F, then by Hooke’s law, the springs extends by:

Spring 1:

Spring 2:

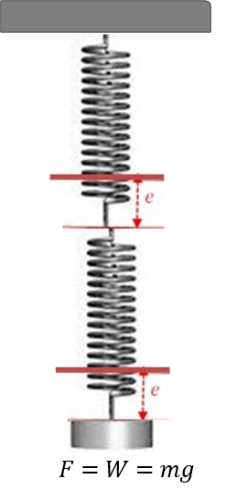
If e be the total extension, then;

Effective spring constant K

If the springs are identical, then k₁ = k₂ = k. then;

Thus, for two identical springs connected in series therefore, the spring constant reduces by half.

If the springs are not identical, then;

Factors affecting spring constant

There are various factors that affect the spring constant:

(i) Length: Spring constant is inversely proportional to length. An increase in length leads to a decrease in the spring constant and vice versa.

(ii) Thickness of the wire making the spring. A thicker wire makes a stiffer spring with a larger spring constant.

(iii) Cross sectional area (diameter) of the spring: A wider spring is less stiff compared to a narrower spring. The greater the cross-sectional area of a spring therefore, the smaller the spring constant.

(iv) Number of active coils (turns) that are free to expand. A spring with relatively more turns is springier hence has a smaller spring constant. 

Experiment to prove Hooke’s law, determine the spring constant;

• Suspend a spring and measure its length (original length) 
• Suspend first mass, measure the new length
• Determine the extension (new length – original length)
• Keep adding more masses and noting the new extension (e) every time.

• Plot a graph of weight (F=mg) against extension (e) – it should be a straight line where the spring obeys Hooke’s - and determine the gradient (k) law. 
• The gradient of the graph represents the string constant.

Stress and Strain

Hooke's law can also be defined in terms of stress and strain as: the stress applied to a material within the elastic limit is proportional to the strain, i.e.    

                                      (i)

Stress refers to the force acting on a unit cross-sectional area of an object. 

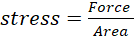                                         (ii)

If the stress causes the length of the object to change, the strain is defined as the ratio of the change in length to the original length;

                        (iii)

Now, consider a wire of length L and cross-sectional area A. Suppose a force F acts on the wire such that its length changes by ∆L.

It follows that;

                                                        (iv)

                                                      (v)

From Hooke’s law;

                                                                  (vii)

                                                              (vii)

Where γ is the constant of proportionality called modulus of elasticity or young’s modulus. 

Because ∆L=e (extension), equation (ix) may be written as;

                                                                (vii)

It is important to note that if the ratio of length of the wire to its cross-sectional area is unity, i.e., L/A =1, Young’s modulus (modulus of elasticity) and spring constant are equal.

Examples

KCSE 2021

(1) Figure 5 shows two identical springs arranged side by side and supporting a weight of 50 N.

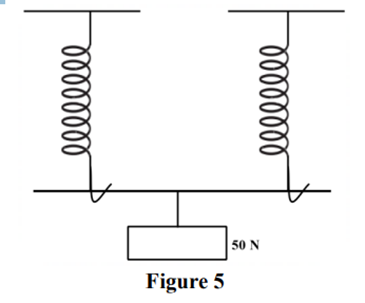
When the same weight is supported by one of the springs above, it produces an extension of 1 cm. Determine the effective spring constant of the arrangement in Figure 5. (3 marks)

Solution

For a parallel arrangement the spring constant is double the spring 

KCSE 2020

None

KCSE 2019

(1) Figure 5 shows two springs C and D of the same length and equal number of turns made from the same wire.

State with a reason which of the two springs can support a heavier load before attaining the elastic limit. (2 marks)

Spring C given that it has a smaller cross-sectional area hence a larger spring constant.

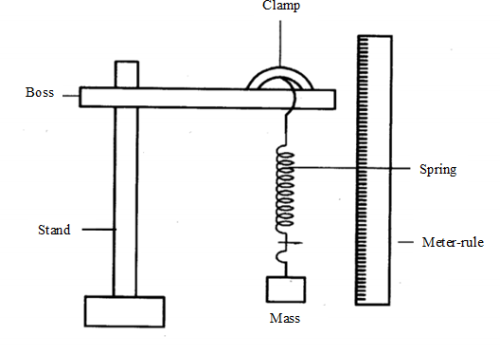
(2) A student is provided with five 20g masses, a meter rule, a spring with a pointer, a stand, a boss and a clamp.

(i) In the space provided, sketch a labelled diagram of the setup that may be used in order to verify Hooke’s law using this apparatus. (3 marks)

(ii) State two measurements that should be recorded in order to plot a suitable graph so as to verify Hooke’s law. (2 marks)

• Weight (force) after masses are mass hung.
• Extension produced by every set of masses

(iii) Describe how the measurements made in (ii) can be used to determine the spring constant. (2 marks)

• Arrange the apparatus as shown in (i) above.
• Suspend first mass, measure the new length
• Determine the extension 
• Keep adding more masses and noting the weight (F) and new extension () every time.
• Plot a graph of weight against extension (it should be a straight line where the spring obeys Hooke’s law). 
• Determine the gradient (k) of the linear part
• The gradient represents the spring constant

(3) A helical spring stretches by 0.6 cm when supporting a weight of 40 g. Determine the extension when the same spring supports a weight of 65 g. (3 marks)

Determine spring constant first;

Then;

KCSE 2018

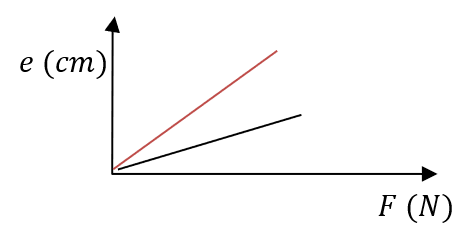
(1) Figure 8 shows the graph of extension against force for a certain helical spring. On the same diagram sketch the graph of extension against force for a spring with a lower value of spring constant. (1 mark)

KCSE 2017

(1) A student was provided with several identical masses, a metre rule, a spring and a stand, boss and clamp. Outline five steps that the student should follow in order to verify Hooke’s law. (5 marks)

• Measure length of spring
• Suspend first mass, measure the new length
• Determine the extension
• Keep adding more masses and noting the new extension (e) 
• Plot a graph of weight F against extension and determine the gradient k
• Hooke’s law:

(2) Figure 4 shows a graph that was drawn from the results obtained in an experiment to study the extension of a spring.

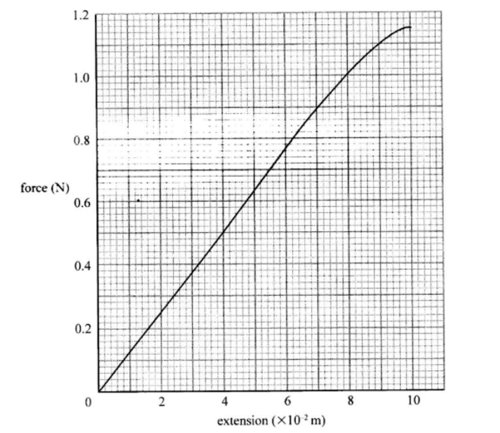
From the graph determine:

(i) The spring constant K. (3 marks)

(ii) The load that causes an extension of 3 x 10^-2 m. (1 mark)

Use formula, 

or get answer directly from graph

(3) Three identical springs of spring constant 100 Nm^-1 are arranged as shown in Figure 5 to support a 5N load. 

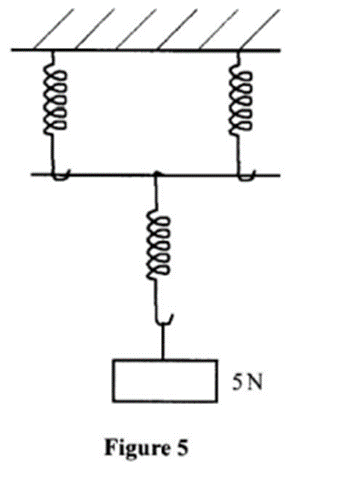
Determine the total extension for the arrangement 

parallel arrangement

Series arrangement

By Hooke's law;

Revision Questions

KCSE 2016

(1) The three springs shown in Figure 7 are identical and have negligible weight. The extension produced on the system of springs is 20cm.

Determine the spring constant of each spring. (2 marks)

KCSE 2015

(1) A spring extends by 6 cm when supporting a mass of 0.06 kg on earth. When the spring is used to support the same mass on the moon, it extends by 1 cm. Determine the moon’s gravitational strength. ( Take gravitational field strength on earth as I0 Nkg-¹) (3 marks)

KCSE 2014

(1) A light spiral spring extends by 4 mm when loaded with a weight W. The spring is connected in series with an identical spring. The combination is loaded with the weight W. Determine the extension of the combination. (2 marks)

KCSE 2013

(1) An object of weight 20 N attached at the end of a spring causes an extension of 0.5 cm on the spring.

(a) Determine the spring constant of the spring. (2 marks)

(b) Determine the weight of an object that would cause an extension of 0.86 cm when attached at the end of the same spring. (1 mark) 

KCSE 2012

91) Table 1 shows the results of an experiment carried out to study the properties of a spring. 
Table 1

State with a reason whether the experiment was done within the elastic limit of the spring. (2 marks)

KCSE 2011

Figure 2 shows a spring balance. It’s spring constant is l25Nm^-1. The scale spreads over

Determine the maximum weight that can be measured using this spring. (3 marks)

KCSE 2010

(1) State the Sl unit of a spring constant.     (1 mark)

Dr. Margaret W. Chege